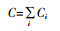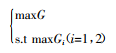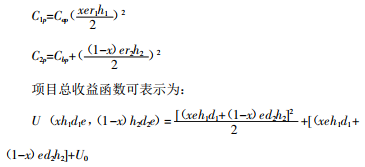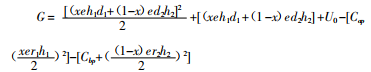【摘要】PPP项目运营期长,参与方众多;在项目建设和运营的过程中,容易对社会公众产生较大的影响,增加社会的不稳定性。在这种情况下,保护PPP项目的公共利益就显得至关重要。论文基于动态博弈,讨论了完全信息博弈中在PPP项目中政府部门和社会资本如何确定公共利益保护的划分比例,以及在确定分配比例的基础上,如何选择双方的努力程度。理论推导结果展示,政府部门和社会资本的公共利益分配比例与双方的贡献程度、收益分配比例成正比,与双方保护公共利益的成本成反比。此外,分配较多公共利益保护份额的一方在项目建设中倾向于减少自己的投入水平。
【关键词】PPP项目;公共利益;动态博弈论
1引言
PPP项目利益相关方众多,参与方众多,各方在项目过程中追求不同目标,因此会产生一定的纠纷。PPP项目的参与者都是PPP项目的利益相关方,其中主要包括政府、项目发起人、项目承包商、项目运营商、专业咨询团队等。每方扮演的角色不同,追求的目标不尽相同。其中,可以直接影响PPP项目治理过程的相关方主要为政府部门和私人部门[1]。
在实际运营过程中,双方的利益诉求难以统一,双方的合作往往依靠合约的制定、关系规范的制定以及互相信任而产生,双方在选择策略行动时,往往考虑自身利益的最大化,即存在“个体理性”的问题。而由于双方的地位、管理模式、技术水平、信息了解途径等不尽相同,在实际运营过程中,双方可能会相互隐瞒一些重要信息,例如政府对项目收益的夸大,私人部门为了获取合作而隐瞒其财政等方面的负面信息。这里,就出现了“不完全信息动态博弈”的情况[2][3]。
在不完全信息博弈中,参与者对其他参与者的类型、策略空间及损益函数的信息了解得不够准确,或者不是对所有其他参与者的类型、策略空间及损益函数的信息有清晰的了解。在不完全信息动态博弈中,一开始参与者根据其他参与者的不同类型和所属类型的概率分布,建立起自己的初步判断。在博弈开始后,该参与者根据其观察到的其他参与者的行动,不断肯定或修正自己的判断,并且根据这种判断选择对自己最有利的行动。
政府部门和私人部门针对PPP项目公共利益保护的博弈过程分为两个阶段。第一个阶段为“合作阶段”,政府和私人部门通过对项目基本情况的了解以及对项目涉及公共利益的评估,共同确定一个双方可以认可的公共利益保护分配方案。第二个阶段为“对抗阶段”,在确定双方各自公共利益保护的比例下,双方分别对项目作出自己的努力水平,使得自身收益最大。
从这里可以看出,通过博弈过程的建立,该博弈过程需要着重解决两个问题。第一个问题是,在合作阶段,政府部门和私人部门的均衡的公共利益保护分配比例如何划分;第二个问题,在对抗阶段,政府部门和私人部门如何选择自己的最优策略(对公共利益保护的投入水平),以达到自身利益的最大化。
2博弈模型的构建
在PPP项目中,政府部门和私人部门博弈,以达到自身利益的最大化。自身利益就是项目的总净收益,即收益中去掉成本的净额。公共利益的保护和项目绩效有着正向关系,因此保护公共利益在一定程度上也增加了项目的收益。从另外一个角度说,如果项目的公共利益不能得到保障,项目可能会对相关社会民众的生活带来一定的影响,甚至引发社会冲突,这会对政府和私人部门的收益带来不良影响;而公共功能和公共需求的保障也是PPP项目运营期获取收益的重点内容,如果项目的公共功能和公共需求不能得到保障,项目的盈利更难以得到保障。从这个角度说,保护公共利益无论是对于政府部门或是私人部门,都会带来其自身的收益。虽然这种收益可能不会当期立刻反应到以货币为衡量单位的金钱上,但这种收益是切实存在的。
在PPP项目中,政府部门和私人部门博弈,以达到自身利益的最大化。自身利益就是项目的总净收益,即收益中去掉成本的净额。假设项目在特许运营期间的总收益函数为U,参与方的收益为Ui,其中包含两个部分,基础收益Uib和保护公共利益所带来的收益Uip。假设分配给私人部门的收益比例为(1-k)(0i。我们假设其中包含两个部分:基础成本Cib和用于公共利益保护的成本Cip,则项目总投入
由以上的假设可以得到项目的总净收益。设项目的总净收益为G,私人部门通过分配方案获得的收益为Gi(i=1,2)。则有:
G=U-C
G1=kU1-C1
G2=(1-k)U2-C2
项目的公共利益保护e对项目收益有着正向影响,即G随着e的增加而增加。而由边际效用递减知,G为凹函数,G随着e的增加的递增程度递减。则有,
将信息不对称的公共利益保护博弈转化为求解一定约束条件下的项目整体净收益最大问题,建立如下分配模型:
3模型的求解
3.1求解思路
本模型的关键是求解PPP项目公共利益分配中政府部门和私人部门在均衡状态下对公共利益的分配比例x,以及在该分配比例下,政府部门和私人部门在公共利益保护时的投入水平的确定。
这是一个多阶段的博弈问题,采用逆推归纳法求解此问题。首先,假设公共利益的分配比例x已经确定,分析在均衡状态下,政府和私人部门为使自身收益最大化而做出的理性决策对自己的公共利益保护水平的确定,对收益函数求导,求出在分配比例确定情况下政府部门和私人部门收益最大时的公共利益保护投入水平。之后,将该公共利益保护投入水平带入收益方程,求导,得出非对称信息下政府和私人部门双方的均衡公共利益分配比例。
3.2假定公共利益分配比例x求解双方最优投入水平
假定x已经确定,求解在均衡条件下,政府和私人部门为自身收益最大化对保护公共利益的投入水平。这里设需要保护的公共利益总和为e,设d1,d2分别为政府和私营资本对项目建设和经营的贡献。设r1,r2分别为政府和私营资本双方的公共利益保护成本系数。则可得,
G=U(xh1d1e,(1-x)h2d2e)-(C1b+C1p)-(C2b+C2p)
G1=kU(xh1d1e,(1-x)h2d2e)-(C1b+C1p)
G2=(1-k)U(xh1d1e,(1-x)h2d2e)-(C2b+C2p)
同时假定,政府和私人部门的总收益和成本为投入水平的二次函数,参考文献中的公式:
Cap,Cbp,U0均为常数,为了后面的运算的方便,取系数值为1/2,此时,项目总收益函数:
政府的收益为:
假定已确定分配方案x,分析双方的理性水平。根据最优原则,
4结语
通过以上分析可以发现,政府部门和私人部门对于项目公共利益保护的投入程度具有以下特点。
①政府与私人部门在对抗阶段对于项目公共利益保护的投入程度与他们在合作阶段对公共利益保护的分配比例成反比,即在合作阶段承担较多公共利益保护的参与方倾向于在对抗阶段减小对公共利益保护的投入承担,而在合作阶段承担较少公共利益保护的参与方倾向于在对抗阶段增加对公共利益保护的投入承担。
②双方对项目的投入水平与其收益分配水平成正比,即获取收益分配份额高的一方会对项目公共利益保护付出更高的投入水平。
③政府和私人部门对项目公共利益的投入水平与其对项目所作出的贡献成正相关。即投资比例越高,承担的风险越大,这一方就更有意愿对项目公共利益进行保护,增加其投入比例。
④政府部门和私人部门对项目公共利益的投入水平和公共利益保护的成本成反比,即保护公共利益需要耗费更多成本的一方会选择较小的公共利益投入水平。
⑤政府与私人部门在对抗阶段对于项目公共利益保护的投入程度与他们在合作阶段对公共利益保护的分配比例成反比,即在合作阶段承担较多公共利益保护的参与方倾向于在对抗阶段减小对公共利益保护的投入承担,而在合作阶段承担较少公共利益保护的参与方倾向于在对抗阶段增加对公共利益保护的投入承担;讨论其中的极值情况,当X=0,私人部门承担全部公共利益保护时,政府部门在对抗阶段需进行的投入程度为无限大,而私人部门投入程度为一个确定的数值,此时他的投入程度只与总公共利益保护内容、双方的收益分配水平、双方的贡献程度和保护成本有关。反之。当X=1,政府部门承担全部的公共利益保护时,私人部门在对抗阶段的投入程度为无限大,而政府部门需进行的投入程度为一确定的数值。
⑥双方对项目的投入水平与其收益分配水平成正比,即获取收益分配份额高的一方会对项目公共利益保护付出更高的投入水平;此时,如果k=0,即政府部门不获取任何收益,则政府部门在对抗阶段倾向于付出的投入程度无限小,由私人部门对公共利益保护进行努力,这种情形在实际情况可能出现;而k=1,即私人部门不获取任何收益,这种项目在实际中不可能出现。
⑦政府和私人部门对项目公共利益的投入水平与其对项目所作出的贡献成正相关。即投资比例越高,承担的风险越大,这一方就更有意愿对项目公共利益进行保护,增加其投入比例。
⑧政府部门和私人部门对项目公共利益的投入水平和公共利益保护的成本成反比,即保护公共利益需要耗费更多成本的一方会选择较小的公共利益投入水平。
【参考文献】
【1】章昆昌.基于博弈论的PPP项目风险分担方法研究[D].长沙:湖南大学,2011.
【2】施锡铨.博弈论[M].上海:上海财经大学出版社,2000.
【3】刘洪积.基于博弈论的PPP模式收益分配研究[D].成都:西南交通大学,2010.