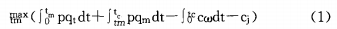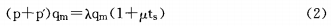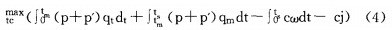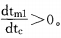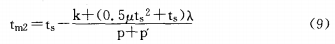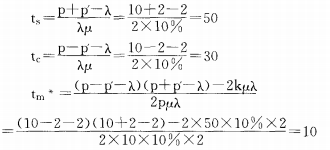摘要:确定高速公路建设规模是高速公路建设的重要环节,在修建高速公路BOT项目时,项目公司考虑的是企业利润最大化,而政府考虑的是社会整体福利的最大化。政府确定给予项目公司的特许期,而项目公司确定高速公路的投资规模,在社会福利最大化约束条件下和随着时间增加高速公路需求不断增长情况下,用博弈论方法建立了高速公路BOT项目进行投资规模决策和特许权期的确定的模型,求得了高速公路的最优投资规模和政府给予项目公司的最优特许期。
关键词:高速公路;BOT;项目规模;特许权期
O引言
随着我国深化改革不断加快和经济不断发展,各地高速公路项目需求不断增加。高速公路不仅给各地的交通运输带来的便利,也带动了相关区域的国民经济,是衡量国民经济现代化的重要标志之一。但各地区在高速公路修建中普遍面临着融资难题。高速公路项目的修建周期长、成本回收时间长、资金需求量大等这些原也成为了制约各地方发展高速公路的难题。在此背景下发改委和财政部力推包括)T在内的PPP模式,引进更多社会资本投入到高速公路建设和运营中。BOT模式是政府将一个工程项目的投资、建设和运营等特许权在特许权期内授予项目公司,等到特许权期期满之后,项目公司将项目无条件移交给政府的融资模式。运用BOT模式能够引入民问资本投入到高速公路建设中,提前满足社会和民众的交通出行需求,而且政府通过和社会资本合作,学习到先进的管理技术,提高政府管理水平。
高速公路BOT项目自立项建设、运营至移交,一般会经历一个较长的特许权期,在此期间随着经济的高速发展,高速公路的车流量会逐渐增大。在高速公路的设计和修建上,应具有一定的超前规划意识,高速建成通车前期,由于车流量处于不足状况,高速公路项目的经济效益还不能体现,但区域经济的不断增长,高速公路的通行量会不断上升,高速公路投资规模过小,就会在建成通车后很快就满足不了交通需求,不得不修建另一条高速公路或改扩建。然而在修建高速公路BOT项目时,项目公司会向政府取得一个限制竞争保证,使得修建新公路困难重重,因此高速公路的建设规模应考虑到较长远经济发展的需要,在设计建设前就应当确定合理的投资规模。如何确定合理的投资规模,发挥政府资源配置的作用,保证项目的社会效益和项目公司利益,实现公私合作共赢,对政府和项目公司都具有一定积极的理论意义和现实意义。
1问题描述及决策模型建立
1.1问题描述
一般情况来说,高速公路的修建成本都较大,修建周期也较长,政府不会在同一区域短时间内规划建设新的高速公路,故政府在设计、建设前就应规划、预估合理的投资规模。若是BOT项目公司考虑到未来的通车量会逐年增加而扩大高速公路投资规模,相应的总收入会因通车量增加而增加,而与之相应建设成本和运营及维护成本也会相应提升,而且高速公路的投资规模一旦确定,在通车量未能达到饱和的这一段时间里将会带来其通车能力闲置,这都需要项目公司进行权衡。
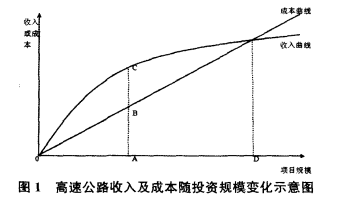
图1表示的是高速公路的成本和收入随高速公路投资规模的变化情况,其中的收入曲线表示)T项目公司的总收入随投资规模的变化情况;成本曲线表示其高速公路的建设成本、运营及维护成本的总和随投资规模的变化情况;项目收入曲线与成本曲线的之间的差就是该规模下BOT项目公司的净收益。项目公司在A点获得净收益AC—AB=BC,D点相应的投资规模比A点大,但其净收益却为零;所以高速公路BOT项目公司会选择A点相对于的投资规模,其项目公司带来最大净收益。
1.2模型建立
高速公路采用BOT方式进行修建及运营,设计总寿命为ts,政府给予项目公司的特许权期(不舍建设期的项目特许期)为tc。高速公路通车量随时间不断增加,设t时刻的通车量为qt=α+ βt,α为高速公路建成时的初始通车量、β为通车量随时间的增长系数。投资规模决定其最大通车量qm=α+ βtm,tm为高速公路通车量达到饱和的时间。设高速公路建设成本cj和年运营及维护成本Cw与最大通车量qm的关系分别为cj=kqm、cω= λqm(1+υt),K是高速公路建设成本系数,λ是初始运营及维护成本系数,υ为运营及维护成本随时问的增长系数(随运营时间增长,运营及维护成本逐步增长),k、λ、υ皆为常数。车辆通车费用为P,参数α、β、k、λ、ω和P均大于0。
政府确定给予项目公司特许期的长短,而项目公司决定高速公路投资规模大小,也就是决定高速公路最大通车量,进而决定通车量达到饱和的时间tm,这相当于将其转化为了对tm的选择来确定投资规模。项目公司从自身收益考虑,选择的修建规模最多也只会满足特许期期满那一时刻高速公路通车需求所达到的最大投资规模,即有tm≦tc。
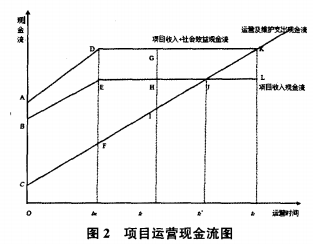
根据上述假设和1.1节中的分析,BOT项目公司投资决策是选择tm,使其B0T项目公司净收益达到最大,即图2中多边形BEHIC表示的部分减去项目建设成本cj最大化,所以项目公司的投资规模决策模型为:
式(1)的涵义是选择tm,也就是bot项目公司选择最佳投资规模使项目公司自身收益最大化。第一项表示从特许经营期(不计建设期)开始到通行量达到最大时的tm的总收入,第二项表示从tm之后直到tc的总收入,第三项表示tc时间内总的高速公路运营及维护成本,第四项表示高速公路项目的建设成本。
在图2中,在[tc,ts]区间政府收益不断增加,在ts时政府收益达到最大。然而高速公路有明显的社会效益,假设单位通车量所带来的社会效益为P。政府在修建高速公路时考虑的是社会整体福利达到最大化,政府会继续运营项目,直到项目收入+社会效益现金流与运营及维护支出现金流相等,在ts时刻结束运营。得:
政府在运营期[tc,ts]区间内,政府其项目直接货币收益不得为负,得:
高速公路有明显的正的外部效应,为使社会福利最大化,即图2中多边形ADKC所表示部分减去项目建设成本cj最大化,即项目所达到的社会福利最大化,政府在决定特许权期时的决策模型是:
式(4)的涵义是政府确定tc,即确定项目的特许权期使社会福利最大化。括号中第一项表示从建设完成,通车开始到刚使通车量达到最大时的tm时刻的总收益,第二项表示从tm以后直到高速公路结束运营的总收益,第三项表示项目生命周期tm内总的运营及维护成本,第四项表示项目的建设成本。
2模型求解及分析
上一节建立了决策模型,下面进行求解。政府先确定高速公路项目公司特许权期,项目公司然后选择投资规模,这是个完全信息动态博弈问题,下面采用逆向归纳法进行求解。由(1)式求最优一阶导数条件得:
在项目的特许权期内单位通车收入P是大于或等于初始单位运营及维护成本的,否则项目公司就无法回收成本,进而得出
随后得出随着tc增大,tml增大。即tc和tml正相关。即随着政府给予项目公司的特许权期增加,项目公司的投资规模在增大。当(2)和(3)联立得:
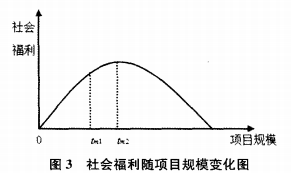
政府可以预测到项目公司将根据式(5)进行投资即项目公司会根据特许权期来确定项目投资,式(4)得出社会福利和的关系如图3,并求得最优一阶导数条件得:
在图3中,可知tm在[O,tm2]区间内项目产生的社会福利随着tm增大而增大,经计算可知无论tml随tc如何变化,都有tml≦tm2恒成立,即政府所希望的高速公路投资规模不是项目公司最优投资规模,政府所希望的高速公路投资规模恒大于项目公司最优投资规模。
证明如下:要证明tml≦tm2
要想社会福利尽量最大化,必须使项目公司最优投资规模尽量接近政府所希望的投资规模,应使tl在保证条件下最大化。又因为tc和tml正相关,所以政府在决定特许权期tc时,在保证政府收益非负的条件下tc应尽可能大,使社会福利即式(4)最大化。得出政府给予项目公司的最优特许权期tc为:
3算例分析
为了更好地说明政府给予项目公司的最优特许期和高速公路的最优投资规模,下面通过算例进行验证。若某高速公路项目采取BOT方式进行运作,设收费价格P为10元,社会效益p为2元。运营及维护成本随时间的增长系数υ为10%,单位初始运营及维护成本系数 λ为2元,单位建设成本系数k为50元。初始通行量α为1.0×107、之后通行量随时间的增长系数β为0.5×106。则根据式(7)、(10)和(11)得
ts=50表明政府选择在50年后结束该高速公路的运营,tc=30表明政府决定的最优特许权期为3O年。tm*=10表明该BOT项目公司选择的高速公路投资规模对应的通车能力刚好能够满足第10年的通车需求。经过计算还可以得到高速公路的建设投资成本cj为7.5亿元,bot项目公司在特许权期内的净收益为15亿元。修建此高速公路后在整个运营期内社会整体福利增加值为37亿。
4结束语
高速公路属于基础设施项目,在这种项目的特许权期确定中,政府不应以自身利益最大化为准则,而是以社会福利最大化作为决策准则。在此原则上政府得高速公路的特许权期,之后项目公司根据政府给予的特许权期来确定高速公路的投资规模。表明高速公路的最优投资规模不是特许权期内达到通车量需求的最大投资规模。政府决定的最优特许权期为政府收益非负的条件下所能达到的最长特许权期,使双方就特许权期确定达成一致,就使项目公司的利润得到了保障,也使社会福利达到了最大化。在此决策下项日公司获得了可观利润,且政府在没有投入财政资金的情况下社会福利得到了改善,达到了公私合作双赢。(本文2017年发表于《现代商贸工业》)